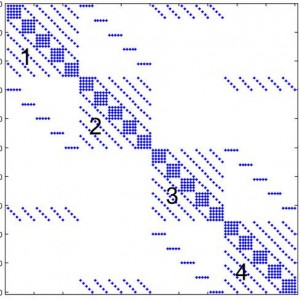
Our existing incompressible Navier-Stokes equation (NSE) solver used in all the above projects employs a spectral multidomain penalty method (SMPM) model only in the vertical direction. By virtue of using a Fourier discretization, the computational domain is always restricted to being periodic in the horizontal with a uniform grid. For the purpose of allowing for more complex boundary conditions and flexibility in localized resolution in one horizontal direction and complex bathymetry, we have been developing a quadrilateral SMPM incompressible NSE solver. The quadrilateral SMPM was first applied to the simpler inviscid shallow water equations. Its implementation in a incompressible NSE framework has been completed for the case of undeformed rectangular subdomains. To this end, in collaboration with Prof. Charles Van Loan in Cornell Comp. Sci., we developed a novel scheme for the iterative solution of the SMPM-discretized pressure Poisson equation (PPE). The associated linear system is non-symmetric, inconsistent and singular giving rise to numerous challenges from a numerical linear algebra standpoint.

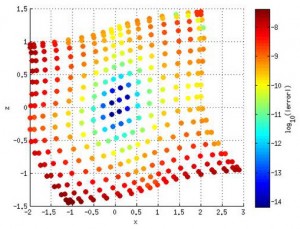We are now in the process of extending the quadrilateral SMPM solver to deformed subdomains, as we progressively overcome challenges arising from the modifications this deformation brings to the highly regular structure of the PPE matrix for the undeformed subdomain case. Following parallelization of the new solver, it will be applied to the study of internal solitary waves shoaling over gentle slopes for the purpose of identifying the associated 2-D and 3-D structural transformations of the waves. In addition, an underwater acoustics model will be coupled to the flow solver to study the propagation of sound through such waves. The PhD student working on this project is Mr. Sumedh Joshi.